1. 两数之和

方法一：暴力枚举

最容易想到的方法是枚举数组中的每一个数x，寻找数组中是否存在 target - x。

当我们使用遍历整个数组的方式寻找 target - x 时，需要注意到每一个位于 x

C 代码解法

/**
 * Note: The returned array must be malloced, assume caller calls free().
 */
int* twoSum(int* nums, int numsSize, int target, int* returnSize){
    for (int i = 0; i < numsSize; ++i){
        for(int j = i + 1; j < numsSize; ++j){
            if (nums[i] + nums[j] == target){
                int* ret = malloc(sizeof(int) * 2);
                ret[0] = i;
                ret[1] = j;
                *returnSize = 2;
                return ret;
            }
        }
    }
    *returnSize = 0;
    return NULL;
}

C++ 代码解法

class Solution {
public:
    vector<int> twoSum(vector<int>& nums, int target) {
        int n = nums.size();
        for (int i = 0; i < n; ++i) {
            for (int j = i + 1; j < n; ++j) {
                if (nums[i] + nums[j] == target) {
                    return {i, j};
                }
            }
        }
        return {};
    }
};

Python3 代码解法

class Solution:
    def twoSum(self, nums: List[int], target: int) -> List[int]:
        n = len(nums)
        for i in range(n):
            for j in range(i + 1, n):
                if nums[i] + nums[j] == target:
                    return [i,j]
        return []

Java 代码解法

class Solution {
    public int[] twoSum(int[] nums, int target) {
        int n = nums.length;
        for(int i = 0; i < n; ++i){
            for(int j = i + 1; j < n; ++j){
                if(nums[0] + nums[1] == target){
                    return new int[]{i,j};
                }
            }
        }
        return new int[0];
    }
}

复杂度分析 时间复杂度：O(N^2)，其中 N 是数组中的元素数量。最坏情况下数组中任意两个数都要被匹配一次。 空间复杂度：O(1)。

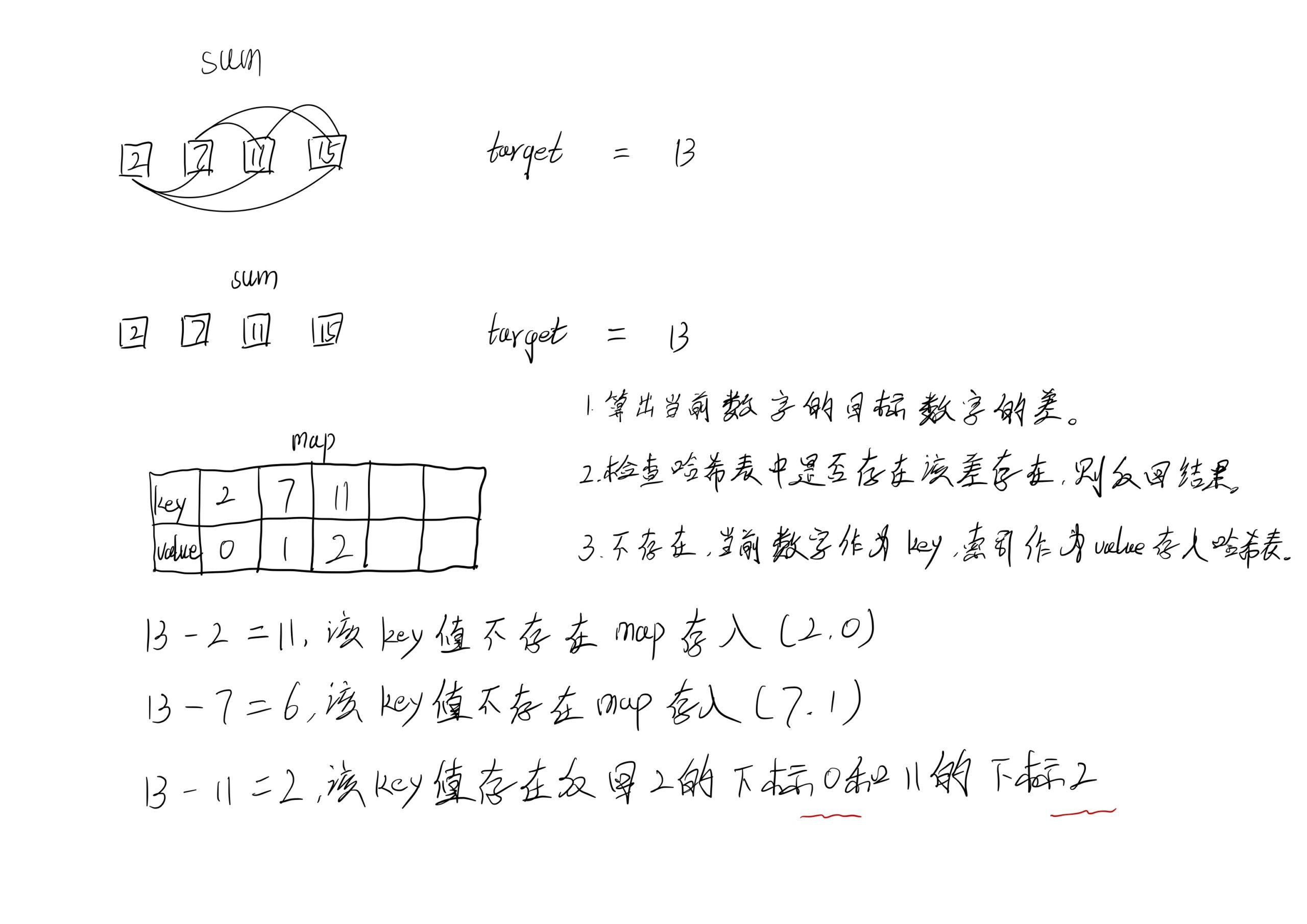
方法二：哈希表

注意到方法一的时间复杂度较高的原因是寻找到 target - x 的时间复杂度过高。因此，我们需要一个更优秀的方法，能够快速寻找数组中是否存在目标元素。如果存在，我们需要找出他的索引。

使用哈希表，可以将寻找 target - x 的时间复杂度降低到从 O(N) 降低到 O(1) 。

这样我们创建一个哈希表，对于每一个 x ，我们首先查询哈希表中是否存在 target - x，然后将 x 插入到哈希表中，即可保证不会让 x 和自己匹配。

Python 代码解法

class Solution:
    def twoSum(self, nums: List[int], target: int) -> List[int]:
        hashtable = dict()
        for i, num in enumerate(nums):
            if target - num in hashtable:
                return [hashtable[target - num], i]
            hashtable[nums[i]] = i
        return []

Java 代码解法

class Solution {
    public int[] twoSum(int[] nums, int target) {
        Map<Integer, Integer> hashtable = new HashMap<Integer, Integer>();
        for (int i = 0; i < nums.length; ++i) {
            if (hashtable.containsKey(target - nums[i])) {
                return new int[]{hashtable.get(target - nums[i]), i};
            }
            hashtable.put(nums[i], i);
        }
        return new int[0];
    }   
}

Source: LeetCode（The title reproduced in this blog is for personal study use only）