Exercise 1-1. Run the “hello world” program on your system. Experiment with leaving out parts of the program, to see what error messages you get.
#include<stdio.h>
main(){
printf("Hello, World\n");
}
Exercise 1-2. Experiment to find out what happens when printf \\’s argument string contains \c, where c is some character not listed above.
#include<stdio.h>
main() {
/*
newline NL (LF) \n backslash \ \
horizontal tab HT \t question mark ? \?
vertical tab VT \v single quote ' \'
backspace BS \b double quote "
carriage return CR \r octal number ooo \ooo
formfeed FF \f hex number hh \xhh
audible alert BEL \a
*/
printf("newline (0x0A): '\n'\n");
printf("horizontal tab (0x09): '\t'\n");
printf("vertical tab (0x0B):'\v'\n");
printf("backspace (0x08): ' \b'\n");
printf("carriage return (0x0D): '\r'\n");
printf("formfeed (0x0C): '\f'\n");
printf("alert (0x07) - added in C89: '\a'\n");
printf("backslash (0x5C): '\'\n");
printf("question mark (0x3F): '\?'\n");
printf("single quote (0x27): '\''\n");
printf("double quote: (0x22)''\n");
printf("octal number (ooo): '\101'\n");
printf("hex number (xhh): '\x41'\n");
}
Exercise 1-3. Modify the temperature conversion program to print a heading above the table.
#include<stdio.h>
/* print Fahrenheit-Celsius table
for fahr = 0, 20, ..., 300; floating-point version */
main() {
float fahr, celsius;
float lower, upper, step;
lower = 0; /* lower limit of temperatuire scale */
upper = 300; /* upper limit */
step = 20; /* step size */
fahr = lower;
printf("Fahrenheit\tCelsius\n");
while (fahr <= upper){
celsius = (5.0 / 9.0) * (fahr - 32.0);
printf("%3.0f\t\t%6.1f\n", fahr, celsius);
fahr = fahr + step;
}
}
Exercise 1-4. Write a program to print the corresponding Celsius to Fahrenheit table.
#include<stdio.h>
main() {
float fahr, celsius;
float lower, upper, step;
lower = 0; /* lower limit of temperatuire scale */
upper = 300; /* upper limit */
step = 20; /* step size */
celsius = lower;
printf("Fahrenheit\tCelsius\n");
while (celsius <= upper){
fahr = (9.0 / 5.0) * celsius + 32.0;
printf("%3.0f\t\t%6.1f\n", celsius, fahr);
celsius = celsius + step;
}
}
Exercise 1-5. Modify the temperature conversion program to print the table in reverse order, that is, from 300 degrees to 0.
#include<stdio.h>
main() {
float fahr, celsius;
float lower, upper, step;
lower = 0; /* lower limit of temperatuire scale */
upper = 300; /* upper limit */
step = 20; /* step size */
fahr = upper;
printf("Fahrenheit\tCelsius\n");
while (fahr >= lower){
celsius = (5.0 / 9.0) * (fahr - 32.0);
printf("%3.0f\t\t%6.1f\n", fahr, celsius);
fahr = fahr - step;
}
}
Exercise 1-6. Verify that the expression getchar() != EOF is 0 or 1.
/* This program prompts for input, and then captures a character
* from the keyboard. If EOF is signalled (typically through a
* control-D or control-Z character, though not necessarily),
* the program prints 0. Otherwise, it prints 1.
*
* If your input stream is buffered (and it probably is), then
* you will need to press the ENTER key before the program will
* respond.
*/
#include<stdio.h>
main() {
printf("Press any key or type CONTROL-Z, then type ENTER. :-)\n\n");
printf("The expression getchar() != EOF evaluates to %d\n", getchar() != EOF);
}
Exercise 1-7. Write a program to print the value of EOF .
#include<stdio.h>
main() {
printf("The value of EOF is %d\n",EOF);
}
Exercise 1-8. Write a program to count blanks, tabs, and newlines.
#include<stdio.h>
main() {
int c, nb, nt, nl;
nb = nt = nl = 0;
while ((c = getchar()) != EOF) {
if (c == ' ') { //ASCII value for " "
++nb;
}
if (c == '\t') { //ASCII value for "\t"
++nt;
}
if (c == '\n') { //ASCII value for "\n"
++nl;
}
}
printf("Total spaces:%d \nTotal tabs:%d \nTotal lines:%d\n", nb, nt, nl);
}
Using ASCII values
#include<stdio.h>
//Using ASCII values
main() {
int c, nb, nt, nl;
nb = nt = nl = 0;
while ((c = getchar()) != EOF) {
if (c == 32) { //ASCII value for " "
++nb;
}
if (c == 9) { //ASCII value for "\t"
++nt;
}
if (c == 10) { //ASCII value for "\n"
++nl;
}
}
printf("Total spaces:%d \nTotal tabs:%d \nTotal lines:%d\n", nb, nt, nl);
}
Exercise 1-9. Write a program to copy its input to its output, replacing each string of one or more blanks by a single blank.
#include<stdio.h>
main() {
char c;
char prev_c; /* previous character */
prev_c = 0;
while ((c = getchar()) != EOF){
/* output c if it's not a blank OR if the previous c is not a blank */
if (c != ' ' || prev_c != ' ') {
putchar(c);
prev_c = c;
}
}
}
Exercise 1-10. Write a program to copy its input to its output, replacing each tab by \t , each backspace by \b , and each backslash by \ . This makes tabs and backspaces visible in an unambiguous way.
#include<stdio.h>
main() {
int c;
while ((c = getchar()) != EOF){
if (c == '\\' || c == '\t' || c == '\b'){
putchar('\\');
if (c == '\\'){
putchar('\\');
}
if (c == '\t'){
putchar('t');
}
if (c == '\b'){
putchar('b');
}
}else{
putchar(c);
}
}
}
Exercise 1-11. How would you test the word count program? What kinds of input are most likely to uncover bugs if there are any?
Exercise 1-12. Write a program that prints its input one word per line.
#include<stdio.h>
#define IN 1
#define OUT 0
main() {
int c, state;
state = OUT;
while ((c = getchar()) != EOF){
if (c == '\n' || c == ' ' || c == '\t'){
if (state == IN){
state = OUT;
putchar('\n');
}
continue;
}
state = IN;
putchar(c);
}
}
Exercise 1-13. Write a program to print a histogram of the lengths of words in its input. It is easy to draw the histogram with the bars horizontal; a vertical orientation is more challenging.
#include<stdio.h>
#define MAXHIST 15 /* max length of histogram */
#define MAXWORD 11 /* max length of a word */
#define IN 1 /* inside a word */
#define OUT 0 /* outside a word */
/* print horizontal histogram */
main() {
int c, i, nc, state;
int len; /* length of each bar */
int maxvalue; /* maximum value for wl[] */
int ovflow; /* number of overflow words */
int wl[MAXWORD]; /* word length counters */
state = OUT;
nc = 0; /* number of chars in a word*/
ovflow = 0; /* number of words >= MAXWORD*/
for (i = 0; i < MAXWORD; ++i){
wl[i] = 0;
}
while ((c = getchar()) != EOF){
if (c == ' ' || c == '\n' || c == '\t'){
state = OUT;
if (nc > 0){
if (nc < MAXWORD) {
++wl[nc];
} else {
++ovflow;
}
}
nc = 0;
}else if(state == OUT){
state = IN;
nc = 1; /* beginning of a new word */
}else{
++nc; /* inside a word */
}
}
maxvalue = 0;
for (i = 1; i < MAXWORD; ++i){
if (wl[i] > maxvalue){
maxvalue = wl[i];
}
}
for (i = 1; i < MAXWORD; ++i) {
printf("%5d - %5d : ", i, wl[i]);
if (wl[i] > 0) {
if ((len = wl[i] * MAXHIST / maxvalue) <= 0) {
len = 1;
}
} else {
len = 0;
}
while (len > 0) {
putchar('*');
--len;
}
putchar('\n');
}
if (ovflow > 0) {
printf("There are %d words >= %d\n", ovflow, MAXWORD);
}
}
Exercise 1-14. Write a program to print a histogram of the frequencies of different characters in its input.
#include<stdio.h>
#include<ctype.h>
#define MAXHISI 15 /* max length of histagram */
#define MAXCHAR 128 /* max different characters */
/* print horizontal histcgram freq. if different characters */
main() {
int c, i;
int len; /* length of each bar */
int maxvalue; /* maximum value for cc[] */
int cc[MAXCHAR]; /* character counters */
for (i = 0; i < MAXCHAR; i++){
cc[i] = 0;
}
while((c = getchar()) != EOF)
if (c < MAXCHAR){
++cc[c];
}
maxvalue = 0;
for (i = 1; i <MAXCHAR; i++){
if (cc[i] > maxvalue){
maxvalue = cc[i];
}
}
for (i = 1; i < MAXCHAR; i++){
if (isprint(i)){ /* isprint(c) printing character including space */
printf("%5d - %c - %5d : ", i, i, cc[i]);
} else {
printf("%5d - - %5d : ", i, cc[i]);
}
if (cc[i] > 0){
if ((len = cc[i] * MAXHISI / MAXCHAR <= 0)) {
len = 1;
}
} else {
len = 0;
}
while (len > 0){
putchar('*');
--len;
}
putchar('\n');
}
}
Exercise 1-15. Rewrite the temperature conversion program of Section 1.2 to use a function for conversion.
#include<stdio.h>
int fahr_celsius(int fahr);
main() {
int i;
for (i = 0; i <= 300; i = i + 20){
printf("%3.1d %6.1d\n", i, fahr_celsius(i));
}
}
int fahr_celsius(int fahr) {
int celsius;
celsius = (5.0 / 9.0) * (fahr - 32.0);
return celsius;
}
Exercise 1-16. Revise the main routine of the longest-line program so it will correctly print the length of arbitrarily long input lines, and as much as possible of the text.
Original code:
#include<stdio.h>
#define MAXLINE 1000 /* maximum input line size */
int getline(char s[], int lim);
void copy(char to[], char from[]);
/* print the longest input line */
main() {
int len; /* current line length */
int max; /* maximum length seen so far */
char line[MAXLINE]; /* current input line */
char longest[MAXLINE]; /* longest line saved here */
max = 0;
while ((len = getline(line,MAXLINE)) > 0){
if (len > max){
max = len;
copy(longest, line);
}
}
if (max > 0){ /* there was a line */
printf("Longest line: %s", longest);
}
return 0;
}
/* getline: read a line into s, return length */
int getline(char s[], int lim) {
int c, i;
for (i = 0; i < lim - 1 && (c = getchar()) != EOF && c != '\n'; i++){
s[i] = c;
}
if (c == '\n'){
s[i] = c;
++i;
}
s[i] = '\0';
return i;
}
/* copy: copy 'from' into 'to'; assume to is big enough */
void copy(char to[], char from[]) {
int i;
i = 0;
while ((to[i] = from[i]) != '\0') {
++i;
}
}
Revised code:
#include<stdio.h>
#define MAXLINE 1000 /* maximum input line size */
int getline(char s[], int lim);
void copy(char to[], char from[]);
/* print the longest input line */
main() {
int len; /* current line length */
int max; /* maximum length seen so far */
char line[MAXLINE]; /* current input line */
char longest[MAXLINE]; /* longest line saved here */
max = 0;
while ((len = getline(line, MAXLINE)) > 0) {
printf("%d %s\n", len, line);
if (len > max) {
max = len;
copy(longest, line);
}
}
if (max > 0) { /* there was a line */
printf("Longest line: %s", longest);
}
return 0;
}
/* getline: read a line into s, return length */
int getline(char s[], int lim) {
int c, i, j = 0;
for (i = 0; (c = getchar()) != EOF && c != '\n'; i++) {
if (i < lim - 2) {
s[j] = c; /* line stall in boundariea */
++j;
}
if (c == '\n') {
s[j] = c;
++j;
++i;
}
}
s[j] = '\0';
return i;
}
/* copy: copy 'from' into 'to'; assume to is big enough */
void copy(char to[], char from[]) {
int i;
i = 0;
while ((to[i] = from[i]) != '\0') {
++i;
}
}
Exercise 1-17. Write a program to print all input lines that are longer than 80 characters.
#include<stdio.h>
#define MAXLINE 1000
#define LONGLINE 80
int getline(char line[], int maxline);
main() {
int len;
char line[MAXLINE];
while ((len = getline(line, MAXLINE)) > 0){
if (len > LONGLINE){
printf("%s", line);
}
}
return 0;
}
int getline(char s[], int lim) {
int c, i, j = 0;
for (i = 0; (c = getchar()) != EOF && c != '\n'; i++){
if (i < lim - 2) {
s[j] = c;
++j;
}
}
if (c == '\n'){
s[j] = c;
++j;
++i;
}
s[j] = '\0';
return i;
}
Exercise 1-18. Write a program to remove all trailing blanks and tabs from each line of input, and to delete entirely blank lines.
#include<stdio.h>
#define MAXLINE 1000 /* maximun input line size */
main() {
char line[MAXLINE]; /* current input line */
while(getline(line, MAXLINE) > 0)
if (remove(line) > 0){
printf("%s", line);
}
return 0;
}
/* getline: read a line into s, return length */
int getline(char line[], int maxline) {
int c, i, j = 0;
for (i = 0; (c = getchar()) != EOF && c != '\n'; i++){
if (i < maxline - 2){
line[j] = c; /* line stall in boundariea */
++j;
}
}
if (c == '\n'){
line[j] = c;
++j;
++i;
}
line[j] = '\0';
return i;
}
/* remove tariling blanks and tabs from character string */
int remove(char s[]) {
int i = 0;
while (s[i] != '\n') { /* find newline character */
++i;
}
--i; /* back off from '\n' */
while (i >= 0 && (s[i] == ' ' || s[i] == '\t')) {
--i;
}
if (i >= 0){ /* is it a nonblank line? */
++i;
s[i] = '\n'; /* put newline character back */
++i;
s[i] = '\0'; /* terminate the string */
}
return i;
}
Exercise 1-19. Write a function reverse(s) that reverses the character string s . Use it to write a program that reverses its input a line at a time.
#include<stdio.h>
#define MAXLINE 1000 /* maximum input line size */
int getline(char line[], int maxline);
void reverse(char s[]);
/* reverse input lines, s line at a time */
main() {
char line[MAXLINE]; /* current input line */
while (getline(line, MAXLINE) > 0){
reverse(line);
printf("%s", line);
}
}
/* getline: read a line into s, return length */
int getline(char line[], int maxline) {
int c, i, j = 0;
for (i = 0; (c = getchar()) != EOF && c != '\n'; i++) {
if (i < maxline - 2) {
line[j] = c; /* line stall in boundariea */
++j;
}
}
if (c == '\n') {
line[j] = c;
++j;
++i;
}
line[j] = '\0';
return i;
}
/* reverse: reverse string */
void reverse(char s[]) {
int i, j;
char temp;
i = 0;
while (s[i] != '\0') { /* find the end of string */
++i;
}
--i; /* back off from '\0' */
if (s[i] == '\n'){
--i; /* leave nawline in place */
}
j = 0; /* beginning of new string */
while (j < i){
temp = s[j];
s[j] = s[i]; /* swap the characters */
s[i] = temp;
--i;
++j;
}
}
Exercise 1-20. Write a program detab that replaces tabs in the input with the proper number of blanks to space to the next tab stop. Assume a fixed set of tab stops, say every n columns. Should n be a variable or a symbolic parameter?
#include<stdio.h>
#define TABINC 8 /* tab increment size */
/* replace tabs with the proper number of blanks */
main() {
int c, nb, pos;
nb = 0; /* number of blanks necessary */
pos = 1; /* position of character in line */
while ((c = getchar()) != EOF){
if (c == '\t'){ /* tab character */
nb = TABINC - (pos - 1) % TABINC;
while (nb > 0){
putchar(' ');
++pos;
--nb;
}
} else if (c == '\n') { /* newline character */
putchar(c);
pos = 1;
} else { /* all other characters*/
putchar(c);
++pos;
}
}
}
Exercise 1-21. Write a program entab that replaces strings of blanks with the minimum number of tabs and blanks to achieve the same spacing. Use the same stops as for detab . When either a tab or a single blank would suffice to reach a tab stop, which should be given preference?
#include<stdio.h>
#define TABINC 8 /* tab increment size */
/* replace strings of blanks with tabs and blanks */
main() {
int c, nb, nt, pos;
nb = 0; /* # of blanks necessary */
nt = 0; /* # of tabs necessary */
for (pos = 1; (c = getchar()) != EOF; ++pos) {
if (c == ' '){
if (pos % TABINC != 0){
++nb; /* increment # of blanks */
} else {
nb = 0; /* reset # of blanks */
++nt; /* one more tab */
}
} else {
for ( ; nt > 0; --nt){
putchar('\t'); /* output tab(s) */
}
if (c == '\t'){
nb = 0;
} else {
for ( ; nb > 0; --nb){
putchar(' ');
}
}
putchar(c);
if (c == '\n'){
pos = 0;
} else if(c == '\t') {
pos = pos + (TABINC - (pos - 1) % TABINC) - 1;
}
}
}
}
Exercise 1-22. Write a program to “fold” long input lines into two or more shorter lines after the last non-blank character that occurs before the n -th column of input. Make sure your program does something intelligent with very long lines, and if there are no blanks or tabs before the specified column.
#include<stdio.h>
#define MAXCOL 10 /* maximum column of input */
#define TABLNC 8 /* tab increment size */
char line[MAXCOL];
int exptab(int pos);
int findblnk(int pos);
int newpos(int pos);
void printl(int pos);
/* fold long input lines into two or more shorter lines */
main() {
int c, pos;
pos = 0; /* position in the line */
while ((c = getchar()) != EOF){
line[pos] = c; /* store current character */
if (c == '\t'){ /* expand tab character */
pos = exptab(pos);
} else if(c == '\n'){
printl(pos); /* print current input line */
pos = 0;
} else if (++pos >= MAXCOL){
pos = findblnk(pos);
printl(pos);
pos = newpos(pos);
; }
}
}
/* printl: print line until pos column */
void printl(int pos) {
int i;
for (i = 0; i < pos; ++i){
putchar(line[i]);
}
if (pos > 0){ /* any chars printed ? */
putchar('\n');
}
}
/* exptab: expand tab into blanks */
int exptab(int pos) {
line[pos] = ' '; /* tab is at least one blank */
for (++pos; pos < MAXCOL && pos % TABLNC != 0; ++pos){
line[pos] = ' ';
}
if (pos < MAXCOL){ /* room left in current line */
return pos;
} else { /* current line is full */
printf(pos);
return 0; /* reset current position */
}
}
/* findblnk: find blank's position */
int findblnk(int pos) {
while (pos > 0 && line[pos] != ' ') {
--pos;
}
if (pos == 0){ /* no blanks in the line? */
return MAXCOL;
} else { /* at least one blank */
return pos + 1; /* position after the blank */
}
}
/* newpos: rearrange line with new position */
int newpos(int pos) {
int i, j;
if (pos <= 0 || pos >= MAXCOL){
return 0; /* nothing to rearrange */
} else {
i = 0;
for (j = pos; j < MAXCOL; ++j){
line[i] = line[j];
++i;
}
return i; /* new position in line */
}
}
Exercise 1-23. Write a program to remove all comments from a C program. Don\\’t forget to handle quoted strings and character constants properly. C comments do not nest.
#include<stdio.h>
void rcomment(int c);
void in_comment(void);
void echo_quote(int c);
/* remove all comments from a valid C program*/
main() {
int c, d;
while ((c = getchar()) != EOF){
rcomment(c);
}
return 0;
}
/* rcomment: read each character, remove the comments */
void rcomment(int c) {
int d;
if (c == '/'){
if ((d = getchar()) == '*') {
in_comment(); /* beginning comment */
} else if (d == '/') {
putchar(c); /* anther slash */
rcomment(d);
} else {
putchar(c); /* not a comment */
putchar(d);
}
} else if (c == '\'' || c == '"') {
echo_quote(c); /* quote begins */
} else {
putchar(c); /* not a comment */
}
}
/* in_comment: inside of a valid comment */
void in_comment(void) {
int c, d;
c = getchar(); /* prev character */
d = getchar(); /* curr character */
while (c != '*' || d != '/'){ /* search for end */
c = d;
d = getchar();
}
}
/* echo_quote: echo characters within quotes */
void echo_quote(int c) {
int d;
putchar(c);
while ((d = getchar()) != c){ /* search for end */
putchar(d);
if (d == '\\'){
putchar(getchar()); /* ignore escape seq */
}
}
putchar(d);
}
Exercise 1-24. Write a program to check a C program for rudimentary syntax errors like unbalanced parentheses, brackets and braces. Don\\’t forget about quotes, both single and double, escape sequences, and comments. (This program is hard if you do it in full generality.)
#include<stdio.h>
int brace, brack, paren;
void in_quote(int c);
void in_comment(void);
void search(int c);
/* rudimentary syntex checker for C programs */
main() {
int c;
extern int brace, brack, paren;
while ((c = getchar()) != EOF) {
if (c == '/') {
if ((c = getchar()) == '*') {
in_comment(); /* inside comment */
}
else {
search(c);
}
} else if (c == '\'' || c == '"') {
in_quote(c); /* inside quote */
} else {
search(c);
}
if (brace < 0) {
printf("Unbalanced braces\n");
brace = 0;
} else if (brack < 0) {
printf("Unbalanced brackets\n");
brack = 0;
} else if (paren < 0) {
printf("Unbalanced parentheses\n");
paren = 0;
}
}
if (brace > 0) {
printf("Unbalanced brackets\n");
}
if (brack > 0) {
printf("Unbalanced brackets\n");
}
if (paren > 0) {
printf("Unbalanced parentheses\n");
}
}
/* search: search for rudimentary syntax errors */
void search(int c) {
extern int brace, brack, paren;
if (c == '{') {
++brace;
}
else if (c == '}') {
--brace;
}
else if (c == '[') {
++brack;
}
else if (c == ']'){
--brack;
}
else if (c == '('){
++paren;
}
else if (c == ')'){
--paren;
}
}
/* in_comment: inside of a valid comment */
void in_comment(void) {
int c, d;
c = getchar(); /* prev character */
d = getchar(); /* curr character */
while (c != '*' || d != '/') { /* search for end */
c = d;
d = getchar();
}
}
/* in_quote: inside quote */
void in_quote(int c) {
int d;
while ((d = getchar()) != c){ /* search end quote */
if (d == '\\') {
getchar(); /* ignore escape seq */
}
}
}

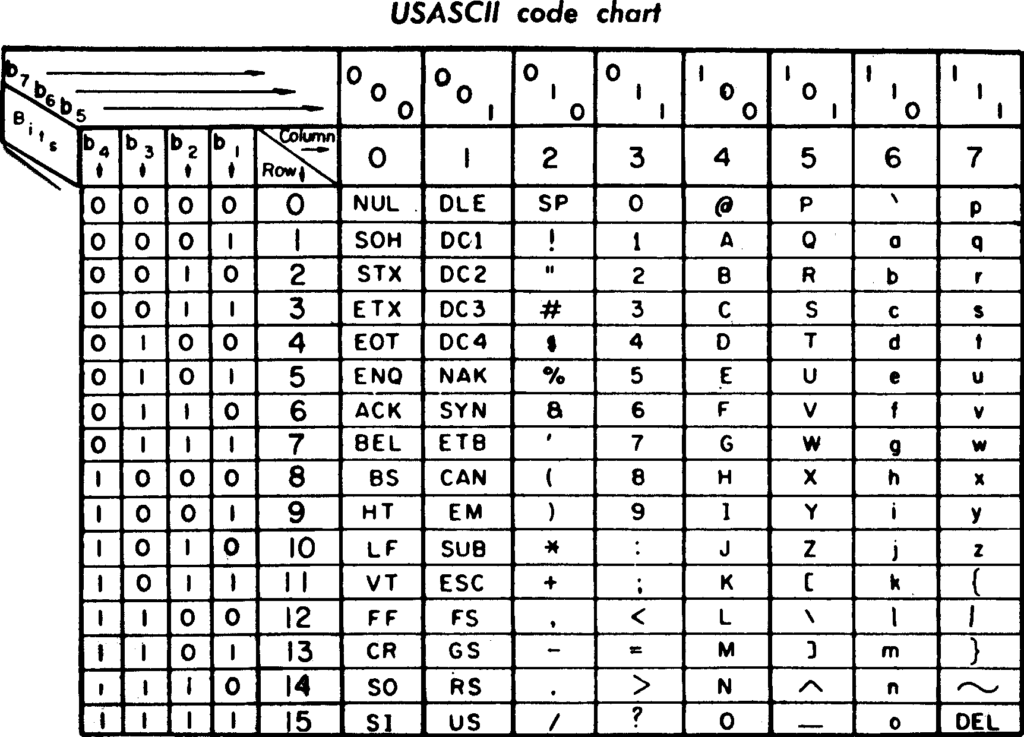 1968年版ASCII编码速见表
1968年版ASCII编码速见表